"El Juego de la Vida" es un autómata celular creado por Conway en los 70’s. Es un juego de cero jugadores en el que los resultados dependen sólo de la posición inicial de las células.
Descripción:
El tablero está dividido en infinitas casillas (posibles poblaciones) que pueden estar vivas o muertas. Una célula tiene 8 células vecinas a su alrededor. Pues bien, una célula muerta "vive" cuando tiene 3 células vecinas vivas, y una célula que está viva, se mantiene con vida sólo si tiene 2 ó 3 células vivas a su alrededor, en cualquier otro caso muere por soledad o por superpoblación. Esta regla se conoce como 23/3, aunque existen otras muchas que dan lugares a otro tipo de poblaciones: caóticas, desoladas, o en el caso de la regla 23/36 a lo que se conoce como HighLife.
La gracia de este juego, que se popularizó en los 80’s, además de que es un poco friki, está en que tiene unas reglas muy sencillas a nivel local o microscópico, pero presenta una enorme complejidad, variedad y riqueza a nivel macroscópico, global o emergente. Tal es así, que se puede configurar como Máquina Universal de Turing, lo que lo hace capaz de resolver cualquier problema computacional que se pueda resolver con un ordenador actual, incluso la simulación de sí mismo.
Se llama Juego de la Vida porque presenta propiedades de catálisis , transporte, estructurales, reguladoras, defensivas e informativas, capaces de simular las bases moleculares de la vida en nuestro planeta. Aunque hoy día no deja de ser un juego, con mucha teoría y estudio detrás, ha popularizado el estudio de otros autómatas celulares que parece que sí que simulan bien el comportamiento de las poblaciones emergentes. El estudio de este tipo de sistemas se usa en el estudio de dinámicas de fluidos (corrientes de líquidos, movimientos de gases, explosiones, flujos de temperaturas), etc. como alternativa a las ecuaciones diferenciales.
Patrones:
Existen varias figuras que presentan comportamientos característicos llamadas patrones:
• Parpadeantes: Oscilan a lo largo del tiempo sin desaparecer.

• Estáticos: figuras que permanecen fijas mientras no se alteren sus células vecinas

• Móviles: Patrones que se van deslizando por la pantalla, el más sencillo es el glider formado por cinco células y cuya figura es hoy en día el símbolo universal de los hackers. Las más complejas se llaman spaceships o naves espaciales.
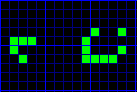
Civilizaciones:
Hay varias civilizaciones que presentan comportamientos peculiares:
• Guns (pistolas): Capaces de crear patrones móviles por sí solos.
• Generadores: Civilizaciones que crecen indefinidamente (Conway premiaba con 50$ a aquél capaz de crear un patrón que creciera cuadráticamente. Se encontraron varios)
• Mathusalenes: Patrones de vida que tardan muchas generaciones en dejar de expandirse para desaparecer o volverse estacionarios.
Como no quiero aburrir con el tema, que es muy interesante, lo dejaré por aquí, y prometo contar más cosas interesantes sobre los autómatas celulares otro día.
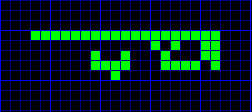
Os dejo el último mathusalen que he descubierto que se vuelve estacionario tras 5652 generaciones. Os recomiendo bajar algún programilla de simulación (gratuitos) , buscar en Internet y empezar a investigar ;)
Descripción:
El tablero está dividido en infinitas casillas (posibles poblaciones) que pueden estar vivas o muertas. Una célula tiene 8 células vecinas a su alrededor. Pues bien, una célula muerta "vive" cuando tiene 3 células vecinas vivas, y una célula que está viva, se mantiene con vida sólo si tiene 2 ó 3 células vivas a su alrededor, en cualquier otro caso muere por soledad o por superpoblación. Esta regla se conoce como 23/3, aunque existen otras muchas que dan lugares a otro tipo de poblaciones: caóticas, desoladas, o en el caso de la regla 23/36 a lo que se conoce como HighLife.
La gracia de este juego, que se popularizó en los 80’s, además de que es un poco friki, está en que tiene unas reglas muy sencillas a nivel local o microscópico, pero presenta una enorme complejidad, variedad y riqueza a nivel macroscópico, global o emergente. Tal es así, que se puede configurar como Máquina Universal de Turing, lo que lo hace capaz de resolver cualquier problema computacional que se pueda resolver con un ordenador actual, incluso la simulación de sí mismo.
Se llama Juego de la Vida porque presenta propiedades de catálisis , transporte, estructurales, reguladoras, defensivas e informativas, capaces de simular las bases moleculares de la vida en nuestro planeta. Aunque hoy día no deja de ser un juego, con mucha teoría y estudio detrás, ha popularizado el estudio de otros autómatas celulares que parece que sí que simulan bien el comportamiento de las poblaciones emergentes. El estudio de este tipo de sistemas se usa en el estudio de dinámicas de fluidos (corrientes de líquidos, movimientos de gases, explosiones, flujos de temperaturas), etc. como alternativa a las ecuaciones diferenciales.
Patrones:
Existen varias figuras que presentan comportamientos característicos llamadas patrones:
• Parpadeantes: Oscilan a lo largo del tiempo sin desaparecer.

• Estáticos: figuras que permanecen fijas mientras no se alteren sus células vecinas

• Móviles: Patrones que se van deslizando por la pantalla, el más sencillo es el glider formado por cinco células y cuya figura es hoy en día el símbolo universal de los hackers. Las más complejas se llaman spaceships o naves espaciales.

Civilizaciones:
Hay varias civilizaciones que presentan comportamientos peculiares:
• Guns (pistolas): Capaces de crear patrones móviles por sí solos.
• Generadores: Civilizaciones que crecen indefinidamente (Conway premiaba con 50$ a aquél capaz de crear un patrón que creciera cuadráticamente. Se encontraron varios)
• Mathusalenes: Patrones de vida que tardan muchas generaciones en dejar de expandirse para desaparecer o volverse estacionarios.
Como no quiero aburrir con el tema, que es muy interesante, lo dejaré por aquí, y prometo contar más cosas interesantes sobre los autómatas celulares otro día.
Os dejo el último mathusalen que he descubierto que se vuelve estacionario tras 5652 generaciones. Os recomiendo bajar algún programilla de simulación (gratuitos) , buscar en Internet y empezar a investigar ;)


1 comentario:
Perdona Cary que haya quitado tu comentario, pero tuve que eliminar el artículo y luego volver a ponerlo (a mano) porque el blog me daba un error al hacer la sindicación XML.
De todas formas pude copiar y pegar tu comentario:
=O
suena bastante interesante!!!
yo nunca había escuchado hablar de este juego =P
ahorita mismo me voy a poner a investigar a ver qué =D
10:23 PM
Publicar un comentario